Zelf het Verbruik Meten

Een systeem om het warmteverbuik in een stadsverwarmingsbuizen af te lezen met simpele temperatuursensoren.

Principe: Het energieverbruik kan worden gemeten als je het temperatuursverschil (in ⁰C) weet en de flow (in liters per seconde). Het vermogen, ofwel het energieverbuik per seconde, wordt bepaald door de drop in ⁰C maal het aantal kilo's of liters water in die tijd en de warmtecapaciteit van het water. Het aantal liters per seconde is de flow, de warmtecapaciteit is een constante factor die voor iedereen gelijk is, dus die doet er bij verhoudingsgewijze kostenverdeling niet toe.

Meetschema

Hieronder is eeen meetschema voor 3 (van 11) woningen getekend. Als voor en achter worden aangesloten doe je dit 2x.

Niet duur: Per woning 3 sensoren, eentje minder voor de laatste, maakt 32 voor 11 woningen, een mooi rond getal in de computerwereld. De sensoren kunnen simpele NTC's zijn, die kosten € 0,21 per stuk. Je kunt 8 sensormetingen verzamelen met 1 Arduino Nano van € 2,75. Voor en achter samen dan 64 x € 0,21 + 8 x € 2,75 = € 35,44 aan componenten. Plus bedrading, printjes, plastichuls.

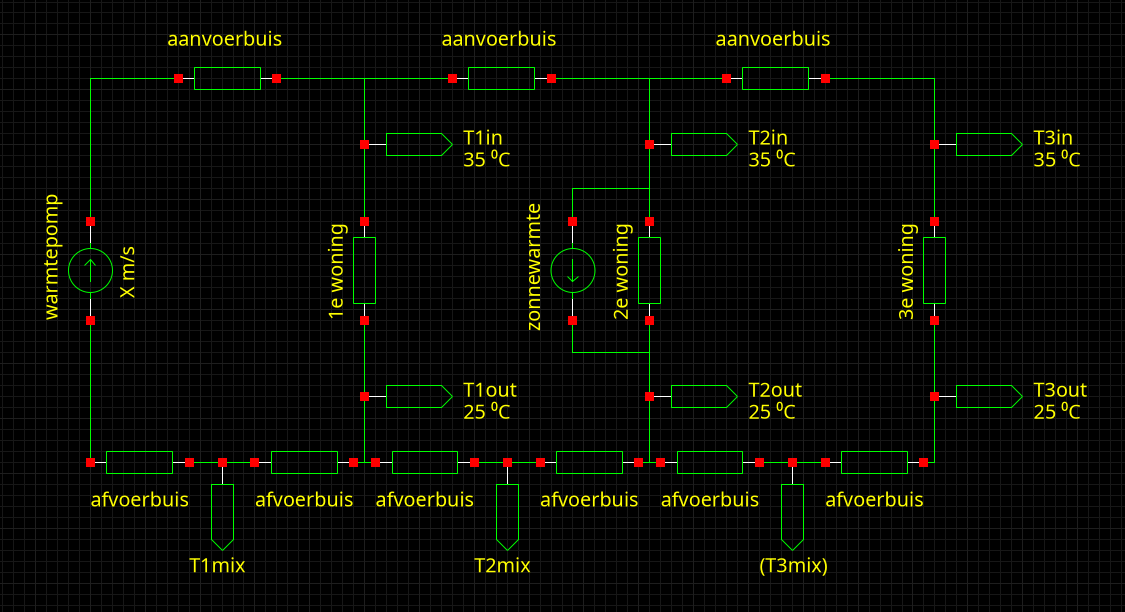
We gaan uit van een warmtepomp die een serie huizen via aan- en afvoerbuizen aanstuurt. De warmtepomp laat weten hoeveel warmte-energie hij produceert (in Watt=W=Joule/seconde=J/s).

Per woning meet je ingaande en uitgaande warmte, Tin en Tout. Je kunt dus van die woning Tin-Tout berekenen, de temperatuurval.

Op de afvoerleiding, halverwege tussen twee woningen, meet je de temperatuur Tmix, dat is het mengsel van alle voorgaande woningen.

Tmix is een mengsel van twee voorgaande leidingen, en de temperatuur wijkt af naar de hardstromende. Daarmee kun je uitrekenen hoe de stroomsnelheden zich verhouden. Omdat de Tmix telkens samenvoegen en uitkomen in de totale stroomsnelheid, kun je zien hoe de totale stroomsnelheid van de warmtepomp zich verdeelt. Daarmee kun je zien wat de stroomsnelheden door de woningen zijn. Als je alleen interesse hebt in de verdeling van warmte gaat het zelfs alleen om de verhouding van stroomsnelheden, en dan hoef je de totale stroomsnelheid niet eens te weten.

Het aandeel afgenomen wamte is de vermenigvuldiging van de temperatuurval Tin-Tout in ⁰C en (het aandeel van) de stroomsnelheid -- en een aantal factoren die voor iedereen gelijk zijn, dus geen invloed hebben op de verdeling.

De energie die naar de warmtepomp gaat bestaat uit:

• Vaste kosten voor het rondpompen wat water door de grond en door de woningen
• Variabele kosten voor het opwerken van de temperatuur

Dit kunt je verdelen zoals het je uitkomt.

Warmer of sneller

Doordat we temperaturen meten kunnen we ook regelen dat alle woningen warmte genoeg krijgen, door de temperatuur op te voeren als dat nodig is. Maar dat betekent wel dat de efficiëntie van de warmtepomp afneemt. Dit is de reden dat deelnemende woningen moeten oppassen niet te veel warmte af te nemen, want dat benadeelt iedereen. Isoleren helpt, een groter oppervlak zoals met vloerverwarming helpt. Meer groepen vloerverwarming parallel zetten helpt ook, die stromen sneller maar onttrekken minder warmte per groep. Als het handiger is om sneller te pompen met dezelfde temperatuur dan is dat veel minder erg omdat de COP maximaal kan blijven. Met deze benadering wordt het principe van flow maal temperatuursdaling dus toegepast als optimalisatiecriterium.

Als je een thermostaat gebruikt dan zal de verwarming zo vaak aanslaan als je nodig hebt. Bij een lagere temperatuur heb je de verwarming gewoon langer open staan. Qua meting maakt dat geen enkel verschil. Optimaal is te proberen dat iedereen nét genoeg warmte krijgt, door de temperatuur te laten zakken tot bij iedereen de thermostaat de verwarming soms even uitschakelt. Zo kun je dus ook meten wie beter of minder geïsoleerd heeft, en dat kan helpen om het gezamenlijk verbruik omlaag te krijgen. Het kan zijn dat nog niet iedereen de woning genoeg heeft geïsoleerd om deel te kunnen nemen.

Aangezien bekend is welke Tin en Tout een woning heeft, en aannemende dat bekend is welke Tmin bij een bepaalde buitentemperatuur nodig is omdat dan de warmte voortdurent doorloopt, zou je van elk woning kunnen uitrekenen welke Tin voldoende zou moeten zijn. Behalve de warmtevraag kun je daarmee ook de vraag naar elektriciteit bepalen, want de gewenste Tin bepaalt de COP. De elektriciteitskosten kunnen verdeeld worden naar verhouding van die elektriciteitsvraag. DIt is een motivatie om te gaan isoleren.

Voorspellen winter

De warmtemeting levert informatie over het verbruik per woning op een bepaald moment. Dit kan worden gecombineerd met de buitentemperatuur op datzelfde moment. Uitgezet in een grafiek levert zoiets een wolk punten rondom een rechte lijn. De meest waarschijnlijke lijn is met statistiek te bepalen, inclusief spreiding. De hoogte van de lijn en zijn helling bieden nuttige informatie over stookgedrag.

Op basis hiervan is te voorspellen hoe de installatie per woning, maar ook voor het netwerk als geheel zich gedraagt als het kouder wordt. Dit kan worden gebuikt om, zonder dat het streng hoeft te vriezen, te bepalen hoe het systeem zich dan zal gedragen. We kunnen de beschikbare gegevens in een dashboard samenvatten, zoals:

OVERZICHT
- Je warmte compenseert verliezen:       50 W/⁰C
- Je energieklasse is daardoor:           C, en 53% van B
- Je verwarmt nu bij buitentemperatuur:   7 ⁰C op 550 Watt

STOOKGEWOONTES
- Je verwarmt onder buitentemperatuur:   11 ⁰C
- Je kamertemperatuur ligt rond:         18 ⁰C
- Je jaarverbruik is ongeveer:           17.000 GJ = 4722 kWh

GEVOLGEN
- Je kunt dit technisch volhouden tot:   -9 ⁰C op 1350 Watt
- Je benadeelt anderen daarmee onder:   -22 ⁰C op 2018 Watt
- Je kamertemperatuur is gezekerd tot:   -9 ⁰C op 1350 Watt
- Je verwarmde ruimte is vorstvrij tot: -22 ⁰C op 2010 Watt

Het vermogen van de warmtepomp ligt vast, en er is een punt waar niet iedereen meer voldoende warmte krijgt. Of waarin een woning zoveel warmte naar zich toe wil trekken dat anderen tekort krijgen. Dit is meestal het gevolg van te weinig isolatie, en dat kan anderen benadelen. Daarom is het belangrijk dit aan te kunnen wijzen, en die persoon ruim op tijd te vragen maatregelen te nemen. Dat kan betekenen dat er beter geïsoleerd wordt, de warmte in een groep of kamer omlaaggedraaid, of desnoods op een andere manier bijverwarmd. Als alles een beetje in balans is met elkaar dan zou dit probleem niet zo snel moeten optreden.

Per woning kan daarvoor afgeleid worden bij welke buitentemperatuur problemen voor die woning of voor andere ontstaan. Dat kan worden gerapporteerd als een minimale tempetatuur waarop die woning voorbereid is. De bewoner kan dan kiezen om hierop in te spelen. Of te overleggen met de anderen.

Het kan spannend lijken om een verwarmbare minimale buitentemperatuur te horen, maar het geeft meer rust dan het niet te weten en er opeens tegenaan te lopen en dan gehaast te moeten ingrijpen. Ook is het nuttig te beseffen dat het gaat om een maximaal verschil tussen de binnen- en buitentemperatuur, maar dat die niet zomaar inklapt. Als het normaal binnenshuis 18 ⁰C kan zijn tot de gemelde buitentemperatuur optreedt, dan zal bij verder dalen de binnentemperatuur ook gaan dalen; maar het vriest dan niet in huis voordat het buiten 18 ⁰C kouder is dan de verwarmbare buitentemperatuur.

Los hiervan kan een temperatuur worden bepaald waarbij de woning meer warmte probeert aan te trekken dan het gelijke deel. Dat is een soort sociale grens, waarbij iemand zich geroepen zou moeten voelen om te isoleren, of iets anders te regelen om niet in die situatie te belanden. Ook dit kan worden voorspeld, en dus ruim op tijd gefixt. Dat is vooral nuttig omdat het heel akelig kan worden als de ene buur het voor anderen onmogelijk maakt voldoende te verwarmen. Deze sociale temperatuur kan boven of onder de verwarmbare buitentemperatuur vallen.

Voor beide temperaturen kan gelden dat ze zo laag zijn dat het er niet toe doet. En dat is ook waarop ontworpen wordt; het pompvermogen wordt bepaald op basis van een verschil van bijvoorbeeld 27 ⁰C tussen binnen- en buitentemperatuur, en dan is een woning op 20 ⁰C te houden tot het buiten -7 ⁰C is. Voor mensen die onder het ontwerpdoel aan W/K vallen is die temperatuur lager; dat geldt ook als het een meerderheid is, of iedereen betreft; de pomp kan namelijk overcapaciteit hebben voor de warmtevraag in W/K.

Terugleveren van warmte

We kunnen besluiten dat teruggeleverde warmte beloond wordt, omdat het de warmtebron "fris" houdt. Er is een maximale teruglevertemperatuur aan de bron (30 ⁰C) en die ontstaat door meer water te mengen met hete zonnecollectoren. Je zou trouwns ook je game-PC met waterkoeling kunnen aansluiten, want die wordt ongeveer 70 ⁰C; de energie van de game-PC wordt dan teruggeleverde warmte. En als je warmte uit je doucheputje wilt gebruiken om warmer water terug te leveren dan kan dat ook, zolang je daarvoor een warmtewisselaar gebuikt.

Vloerverwarming kan ook koelen. Dan wordt de warmtepomp uitgeschakeld (voor iedereen tegelijk) en wordt het koude bronwater meteen door de vloeren gepompt.

Als er evenveel warmte wordt geleverd als afgenomen, dan is het warmtenet alleen maar een simpel rondpompstation, dat kan gratis. Dat klopt met de berekeningen, Tin-Tout is dan nul en de stroomsnelheid doet er dan niet meer toe.

Als er meer warmte wordt teruggeleverd dan afgenomen, dan is Tin-Tout een negatief getal, en de warmteberekening vermenigvuldigt daar wat bij en komt uit op een negatieve afname. De vaste kosten voor het rondpompen blijven positief, maar de variabele kosten worden negatief.

Het mooie aan de bodem is dat die erg langzaam reageert, dus zomerwarmte verfrist de bron terwijl dat in de winter afgenomen kan worden. Er is dus geen reden om zomerwarmte minder waardevol te vinden dan winterwarmte. Bovendien kan het terugleveren dan alleen gebeuren wanneer zonnecollectoren te veel leveren voor je boiler, zodat ook te grote zonnecollectorn niet gaan overkoken, en met een grotere heb je langer profijt van zonnewarmte voor je boiler. Pas als er (ruimschoots) te veel warmte is kan het een probleem worden en moeten we nadenken over een oplossing; een luxeprobleem dus.

Uitzonderingsgeval

Als twee gemengde waterstromen dezelfde uitgangstemperatuur hebben, dan is niet te zien welke harder stroomt. In dat geval kan gekeken worden naar wat anders gebeurt, bijvoorbeeld als niet beide woningen warmte afnemen.

Dit is goed inschatbaar door te kijken naar stookgedrag op andere tijden. Uiteindelijk is zo'n inschatting vaak goed genoeg, vooral als het een aanvulling is over een korte tijd.

Een woning heeft een warmte-afname die bepaald wordt door de gemiddelde binnentemperatuur min de buitentemperatuur, en dat gedeeld door de warmteweerstand van binnen naar buiten. Als de binnentempratuur min of meer constant is dan kun je de verhoudingen tussen woningen bij een bepaalde buitentemperatuur bepalen.

Dit moment kan verfijnd worden natuurlijk. De lichtinval (rechtstreeks uit drie richtingen of diffuus verdeeld) en wind kunnen ook meespelen.

Voor teruglevering geldt de aangenomen lineariteit niet, als van zonneboiler naar bronafgifte wordt omgeschakeld, maar daarvan zijn de vermogens dan wel bekend, en de omschakeling zal abrupt zijn.

Formules

Twee kanalen A en B worden gemengd tot M. Meet de temperatuur van elk, $t_A$, $t_B$ en $t_M$. Weet verder dat de flow de som is, $F_M = F_A+F_B$.

De warmte $E_M=E_A+E_B$ wordt ook gecombineerd:

E_M = E_A + E_B

F_M x T_M = F_A x T_A + F_B x T_B

(F_A+F_B) x T_M = F_A x T_A + F_B x T_B

F_A x (T_M-T_A) = F_B x (T_B-T_M)

F_A:F_B = (T_B-T_M) / (T_M-T_A)

Deze berekeningen zijn minder precies als $'T_M-T-A'$ of $'T_M-T_B'$ rond nul zitten, en onmogelijk als ze nul zijn. In dat geval kun je statistische gegevens over de verhoudingen gebruiken.

Ga uit van binnentemperatuur $'T_{int}'$ en buitentemperatuur $'T_{env}'$, dan is het warmteverlies $'P_{out}'$ dat verschil gedeeld door de thermische weerstand $'R_{th}'$ van de verwarmde delen van de woning. We zagen al dat de opgenomen warrmte $'P_{in}'$ evenredig is met $'T_{in}-T_{out}'$ en met de flow $f$. Verder is uiteraard $'P_{in}=P_{out}'$.

Dan kun je het stookgedrag middelen als $'F x (T_{in}-T_{out}) / (T_{int}-T_{env}'$; de thermische weerstand $'R_{th]'$ is onderdeel van dat stookgedrag; wie slecht isoleert verliest meer energie die moet worden aangevuld.

De statistische analyse per woning naar stookgedrag komt neer op het bepalen van het lineaire verband tussen $'F x (T_{in}-T_{out})'$ en $'T_{env}'$ met lineaire regressie. Dat is dus het energieverbruik als functie van de buitentemperatuur, dat is dus netjes lineair gerelateerd. De uitkomst is een richtingscoefficiënt en een offset, waarmee de woningen met elkaar vergeleken kunnen worden, en waarmee ook in een gegeven weersomstandigheid kan worden gekeken hoe woningen zich onderling gedragen. De offset geeft een indicatie van de gewenste binnentemperatuur en de richtingscoëfficiënt geeft aan hoe goed de isolatie van de woning is.

De beide berekeningswijzen hebben een onzekerheid rond zich, die uit de statistiek volgt. Overigens is de rechtstreeks $F_A:F_B$ methode meestal erg betrouwbaar, en heeft maar heel soms aanvulling nodig uit historische/statistische gegevens. Maar de twee methodes kunnen daarvoor netjes worden gecombineerd om de beste zekerheid te bereiken; het minst zekere heeft dan ook de minste invloed, en dat op een nette glijdende schaal naar statistische principes.

Dit model kan verfijnd worden, bijvoorbeeld met wind en zonlicht uit de drie richtingen (of diffuus).